About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 369 results for "Jonathan Marino" clear search
Foundress dilemma model
Marco Janssen Takao Sasaki Zachary Joseph Shaffer Stephen Pratt Brian Haney Jennifer Fewell | Published Thursday, July 28, 2016A haystack-style model of group selection to capture the essential features of colony foundation for queens of the ant based on observation of the ant Pogonomyrmex californicus.
This is the R code of the mathematical model that includes the decision making formulations for artificial agents. Plus, the code for graphical output is also added to the original code.
Managing Connectivity: insights from modelling species interactions accross multiple scales in an idealized landscape
Marco Janssen Michael Schoon Jacopo A. Baggio Kehinde Salau | Published Monday, October 01, 2012 | Last modified Monday, January 20, 2014The model objective’s is to explore the management choice set to uncover which subsets of strategies are most effective at maximizing species coexistence on a fragmented landscape.
Livestock drought insurance model
Birgit Müller Felix John Jürgen Groeneveld Karin Frank Russell Toth | Published Tuesday, December 19, 2017 | Last modified Saturday, April 14, 2018The model analyzes the economic and ecological effects of a provision of livestock drought insurance for dryland pastoralists. More precisely, it yields qualitative insights into how long-term herd and pasture dynamics change through insurance.
This model extends the original Artifical Anasazi (AA) model to include individual agents, who vary in age and sex, and are aggregated into households. This allows more realistic simulations of population dynamics within the Long House Valley of Arizona from AD 800 to 1350 than are possible in the original model. The parts of this model that are directly derived from the AA model are based on Janssen’s 1999 Netlogo implementation of the model; the code for all extensions and adaptations in the model described here (the Artificial Long House Valley (ALHV) model) have been written by the authors. The AA model included only ideal and homogeneous “individuals” who do not participate in the population processes (e.g., birth and death)–these processes were assumed to act on entire households only. The ALHV model incorporates actual individual agents and all demographic processes affect these individuals. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. Thus, the ALHV model is a combination of individual processes (birth and death) and household-level processes (e.g., finding suitable agriculture plots).
As is the case for the AA model, the ALHV model makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original model (from Janssen’s Netlogo implementation) to estimate annual maize productivity of various agricultural zones within the valley. These estimates are used to determine suitable locations for households and farms during each year of the simulation.
Artificial Long House Valley-Black Mesa
Lisa Sattenspiel Amy Warren | Published Thursday, March 19, 2020This model is an extension of the Artificial Long House Valley (ALHV) model developed by the authors (Swedlund et al. 2016; Warren and Sattenspiel 2020). The ALHV model simulates the population dynamics of individuals within the Long House Valley of Arizona from AD 800 to 1350. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. The present version of the model incorporates features of the ALHV model including realistic age-specific fertility and mortality and, in addition, it adds the Black Mesa environment and population, as well as additional methods to allow migration between the two regions.
As is the case for previous versions of the ALHV model as well as the Artificial Anasazi (AA) model from which the ALHV model was derived (Axtell et al. 2002; Janssen 2009), this version makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original AA model to estimate annual maize productivity of various agricultural zones within the Long House Valley. A new environment and associated methods have been developed for Black Mesa. Productivity estimates from both regions are used to determine suitable locations for households and farms during each year of the simulation.
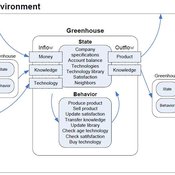
Universal Darwinism in Dutch Greenhouses
Julia Kasmire | Published Wednesday, May 09, 2012 | Last modified Saturday, April 27, 2013An ABM, derived from a case study and a series of surveys with greenhouse growers in the Westland, Netherlands. Experiments using this model showshow that the greenhouse horticulture industry displays diversity, adaptive complexity and an uneven distribution, which all suggest that the industry is an evolving system.
Classical Swine Fever in wild boars
Volker Grimm Stephanie Kramer-Schadt Cédric Scherer Martin Lange Hans-Hermann Thulke | Published Friday, September 06, 2019The model is a combination of a spatially explicit, stochastic, agent-based model for wild boars (Sus scrofa L.) and an epidemiological model for the Classical Swine Fever (CSF) virus infecting the wild boars.
The original model (Kramer-Schadt et al. 2009) was used to assess intrinsic (system immanent host-pathogen interaction and host life-history) and extrinsic (spatial extent and density) factors contributing to the long-term persistence of the disease and has further been used to assess the effects of intrinsic dynamics (Lange et al. 2012a) and indirect transmission (Lange et al. 2016) on the disease course. In an applied context, the model was used to test the efficiency of spatiotemporal vaccination regimes (Lange et al. 2012b) as well as the risk of disease spread in the country of Denmark (Alban et al. 2005).
References: See ODD model description.
Benchmark for DMASON
Andreu Moreno Vendrell Josep Jorba Eduardo César Anna Sikora Cristina Peralta Quesada | Published Friday, November 22, 2024Agent-based modeling and simulation (ABMS) is a class of computational models for simulating the actions and interactions of autonomous agents with the goal of assessing their effects on a system as a whole. Several frameworks for generating parallel ABMS applications have been developed taking advantage of their common characteristics, but there is a lack of a general benchmark for comparing the performance of generated applications. We propose and design a benchmark that takes into consideration the most common characteristics of this type of applications and includes parameters for influencing their relevant performance aspects. We provide an initial implementation of the benchmark for DMASON parallel ABMS platform, and we use it for comparing the applications generated by these platforms.
RiskNetABM
Birgit Müller Jürgen Groeneveld Karin Frank Meike Will Friederike Lenel | Published Monday, July 20, 2020 | Last modified Monday, May 03, 2021The fight against poverty is an urgent global challenge. Microinsurance is promoted as a valuable instrument for buffering income losses due to health or climate-related risks of low-income households in developing countries. However, apart from direct positive effects they can have unintended side effects when insured households lower their contribution to traditional arrangements where risk is shared through private monetary support.
RiskNetABM is an agent-based model that captures dynamics between income losses, insurance payments and informal risk-sharing. The model explicitly includes decisions about informal transfers. It can be used to assess the impact of insurance products and informal risk-sharing arrangements on the resilience of smallholders. Specifically, it allows to analyze whether and how economic needs (i.e. level of living costs) and characteristics of extreme events (i.e. frequency, intensity and type of shock) influence the ability of insurance and informal risk-sharing to buffer income shocks. Two types of behavior with regard to private monetary transfers are explicitly distinguished: (1) all households provide transfers whenever they can afford it and (2) insured households do not show solidarity with their uninsured peers.
The model is stylized and is not used to analyze a particular case study, but represents conditions from several regions with different risk contexts where informal risk-sharing networks between smallholder farmers are prevalent.
…
Displaying 10 of 369 results for "Jonathan Marino" clear search