About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 195 results for "Michel De Garine-Wichatitsky" clear search
Peer reviewed AgModel
Isaac Ullah | Published Friday, December 06, 2024AgModel is an agent-based model of the forager-farmer transition. The model consists of a single software agent that, conceptually, can be thought of as a single hunter-gather community (i.e., a co-residential group that shares in subsistence activities and decision making). The agent has several characteristics, including a population of human foragers, intrinsic birth and death rates, an annual total energy need, and an available amount of foraging labor. The model assumes a central-place foraging strategy in a fixed territory for a two-resource economy: cereal grains and prey animals. The territory has a fixed number of patches, and a starting number of prey. While the model is not spatially explicit, it does assume some spatiality of resources by including search times.
Demographic and environmental components of the simulation occur and are updated at an annual temporal resolution, but foraging decisions are “event” based so that many such decisions will be made in each year. Thus, each new year, the foraging agent must undertake a series of optimal foraging decisions based on its current knowledge of the availability of cereals and prey animals. Other resources are not accounted for in the model directly, but can be assumed for by adjusting the total number of required annual energy intake that the foraging agent uses to calculate its cereal and prey animal foraging decisions. The agent proceeds to balance the net benefits of the chance of finding, processing, and consuming a prey animal, versus that of finding a cereal patch, and processing and consuming that cereal. These decisions continue until the annual kcal target is reached (balanced on the current human population). If the agent consumes all available resources in a given year, it may “starve”. Starvation will affect birth and death rates, as will foraging success, and so the population will increase or decrease according to a probabilistic function (perturbed by some stochasticity) and the agent’s foraging success or failure. The agent is also constrained by labor caps, set by the modeler at model initialization. If the agent expends its yearly budget of person-hours for hunting or foraging, then the agent can no longer do those activities that year, and it may starve.
Foragers choose to either expend their annual labor budget either hunting prey animals or harvesting cereal patches. If the agent chooses to harvest prey animals, they will expend energy searching for and processing prey animals. prey animals search times are density dependent, and the number of prey animals per encounter and handling times can be altered in the model parameterization (e.g. to increase the payoff per encounter). Prey animal populations are also subject to intrinsic birth and death rates with the addition of additional deaths caused by human predation. A small amount of prey animals may “migrate” into the territory each year. This prevents prey animals populations from complete decimation, but also may be used to model increased distances of logistic mobility (or, perhaps, even residential mobility within a larger territory).
…
Modeling financial networks based on interpersonal trust
Michael Roos Anna Klabunde | Published Wednesday, May 29, 2013 | Last modified Thursday, November 28, 2013We build a stylized model of a network of business angel investors and start-up entrepreneurs. Decisions are based on trust as a decision making tool under true uncertainty.
Simple models with different types of complexity
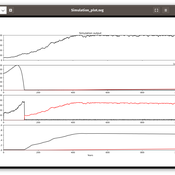
Michael Roos | Published Tuesday, September 17, 2024 | Last modified Saturday, March 01, 2025Hierarchical problem-solving model
The model simulates a hierarchical problem-solving process in which a manager delegates parts of a problem to specialists, who attempt to solve specific aspects based on their unique skills. The goal is to examine how effectively the hierarchical structure works in solving the problem, the total cost of the process, and the resulting solution quality.
Problem-solving random network model
The model simulates a network of agents (generalists) who collaboratively solve a fixed problem by iterating over it and using their individual skills to reduce the problem’s complexity. The goal is to study the dynamics of the problem-solving process, including agent interactions, work cycles, total cost, and solution quality.
This is the final version of the model. To simulate the normative dynamics we used the EmIL (EMergence In the Loop) Framework which was kindly provided by Ulf Lotzmann. http://cfpm.org/EMIL-D5.1.pdf
Social norms and the dominance of Low-doers
Antonio Franco | Published Wednesday, July 13, 2016 | Last modified Sunday, December 02, 2018The code for the paper “Social norms and the dominance of Low-doers”
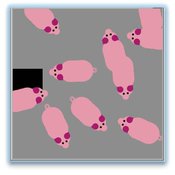
Tail biting behaviour in pigs
Iris J.M.M. Boumans Iris Jmm Boumans | Published Friday, April 22, 2016 | Last modified Wednesday, September 14, 2016The model simulates tail biting behaviour in pigs and how they can turn into a biter and/or victim. The effect of a redirected motivation, behavioural changes in victims and preference to bite a lying pig on tail biting can be tested in the model
Spatial model of the noisy Prisoner's Dilemma with reward shift
Matus Halas | Published Thursday, March 05, 2015 | Last modified Tuesday, May 29, 2018Interactions of players embedded in a closed square lattice are determined by distance and overall gains and they lead to shifts of reward payoff between temptation and punishment. A new winner balancing against threats is ultimately discovered.
Transitions between homophilic and heterophilic modes of cooperation
Genki Ichinose | Published Sunday, June 14, 2015 | Last modified Sunday, November 14, 2021In our model, individual agents are distributed over a two-dimensional square lattice. The agents play the prisoner’s dilemma game with their neighbors, imitate the highest strategy, and then migrate to empty sites based on their tag preference.
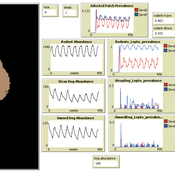
Peer reviewed MHMSLeptoDy (Multi-host, multi-serovar Leptospira Dynamics Model)
Aniruddha Belsare Matthew Gompper Meghan Mason Claudia Munoz-Zanzi | Published Tuesday, January 29, 2019 | Last modified Tuesday, March 12, 2019Leptospirosis is a neglected, bacterial zoonosis with worldwide distribution, primarily a disease of poverty. More than 200 pathogenic serovars of Leptospira bacteria exist, and a variety of species may act as reservoirs for these serovars. Human infection is the result of direct or indirect contact with Leptospira bacteria in the urine of infected animal hosts, primarily livestock, dogs, and rodents. There is increasing evidence that dogs and dog-adapted serovar Canicola play an important role in the burden of leptospirosis in humans in marginalized urban communities. What is needed is a more thorough understanding of the transmission dynamics of Leptospira in these marginalized urban communities, specifically the relative importance of dogs and rodents in the transmission of Leptospira to humans. This understanding will be vital for identifying meaningful intervention strategies.
One of the main objectives of MHMSLeptoDy is to elucidate transmission dynamics of host-adapted Leptospira strains in multi-host system. The model can also be used to evaluate alternate interventions aimed at reducing human infection risk in small-scale communities like urban slums.
Peer reviewed ABM to create populations with realistic Big Five Personality Trait Expressions
Michael Vogrin | Published Tuesday, May 30, 2023This model aims at creating agent populations that have “personalities”, as described by the Big Five Model of Personality. The expression of the Big Five in the agent population has the following properties, so that they resemble real life populations as closely as possible:
-The population mean of each trait is 0.5 on a scale from 0 to 1.
-The population-wide distribution of each trait approximates a normal distribution.
-The intercorrelations of the Big Five are close to those observed in the Literature.
The literature used to fit the model was a publication by Dimitri van der Linden, Jan te Nijenhuis, and Arnold B. Bakker:
…
Displaying 10 of 195 results for "Michel De Garine-Wichatitsky" clear search